The Democracy Paradox: Arrow's Impossibility Theorem
The very essence of a democracy lies in the act of voting and choosing its leaders through elections. An election outcome is supposed to genuinely reflect the will of the people. But does it? Or even, can it? These were some of the questions that Kenneth J. Arrow considered for his Ph.D. in the 1950s. He published his findings, rather disturbing ones, I should add, in his thesis "Social Choice and Individual Values". For his work, Arrow was awarded the Nobel prize in 1972.
When I first encountered Arrow's impossibility theorem, I didn't believe it. It seemed counter intuitive at first sight. However, going through the proof was an enlightening experience. Once I fully grasped it, it was a humbling experience. My dearest ideas of democracy have deep flaws, and the concept of a 'perfect democracy' is fundamentally unattainable. There's nothing we can do about it. If you observe other species in nature, such as lions, gorillas, bees, ants, and more, you'll quickly notice that they have monarchy-like systems with alpha males and queen ants. This makes me wonder: is democracy a failed attempt by us humans to capture the collective will of the people? Does it truly resolve disagreements among us? I am not suggesting that we should revert to monarchy. However, we certainly have much more to uncover in the field of social choice theory. Arrow's impossibility theorem is an excellent starting point to contemplate these questions.
When a Thumbs Down from Commodus isn't Enough!

In the most popular voting scheme, each voter casts one vote for their favourite candidate. The candidate with the highest number of votes is declared the winner. One might wonder: What is wrong with this scheme? To answer this question, let's consider a textbook example of an early election, which is not very different from modern-day elections. On June 24, 105 AD, Pliny the Younger, a Roman senator, wrote a letter to his friend and fellow jurist, Titius Aristo, in which he described a criminal trial. The Senate had to decide the fate of a number of prisoners by voting for their acquittal, exile, or execution. Although acquittal had the largest number of supporters, it did not have a clear majority. Pliny, being in favour of acquittal, argued that the prisoners should be acquitted because it had the highest number of votes. In response, the proponents of harsh punishment strategically moved to withdraw their proposal for execution. As a result, the former supporters of execution now supported for exile, which easily won the majority contest between acquittal and exile.

This example captures many interesting aspects of voting rules. Firstly, people have nuanced opinions; therefore casting just one vote cannot effectively capture the diversity of opinions within a population. It hides a lot of crucial information which is necessary to make decisions which truly reflect the collective will of the people. Furthermore, voters maybe incentivized to cast their vote not for their preferred choice but for a more strategic option that they believe has a better chance of winning. This makes the system lean towards a two-party system and discourages the emergence of alternative, potentially more moderate voices, contributing to political polarization. Single voting also comes with an inherent majority bias.
Setting the Stage: A Mathematical Framework
Maybe single voting is the culprit of all problems in democracy. If so, we should be able to easily fix it. Let's consider a more formal set up for a generalized voting system where instead of one vote per person, we ask them to give their complete preference. Let \(N = \{1,2,\ldots,n\}\) be a set of agents (or voters), and let \(A\) be a finite set of alternatives (or candidates). An agent \(i\) casts her vote by ranking the alternatives from most favorite to least favorite through a strict order \(\succ_i\) on \(A\). A collection of these rankings of all agents is called as a profile given by \(P=(\succ_1,\succ_2\cdots,\succ_n)\). A voting rule is given by a social welfare function (SWF) \(f\) which takes as input a profile \(P\) and gives as output a weak ordering \(\succeq\) on \(A\) - called as the social preference order. Note We that we allow ties in the output, but not in the individual preferences.
Given this setup, what is a good social welfare function? are all the same? Let's check out some of the well studied SWFs. When there are just two candidates, we can apply the majority rule: the candidate preferred by the majority of voters is the winner. When there are more than two candidates, a simple extension of the majority rule is the plurality rule, under which the candidate ranked at the top by the highest number of voters wins. Essentially considering only the top choice of voters, ignoring the subsequent rankings. This is in fact the SWF being followed in most elections. The Roman senate example highlights the problem with this rule. For simplicity, take a look at the following toy example. Four voters rank the candidates: Rani (the one in saree), Liu(wearing hat) and Paul as shown below. Under the plurality rule, Liu would be declared as the winner. But Liu would not win a head to head election against Rani as two out of the four voters prefer Rani over Liu. Then why should Liu be the winner?
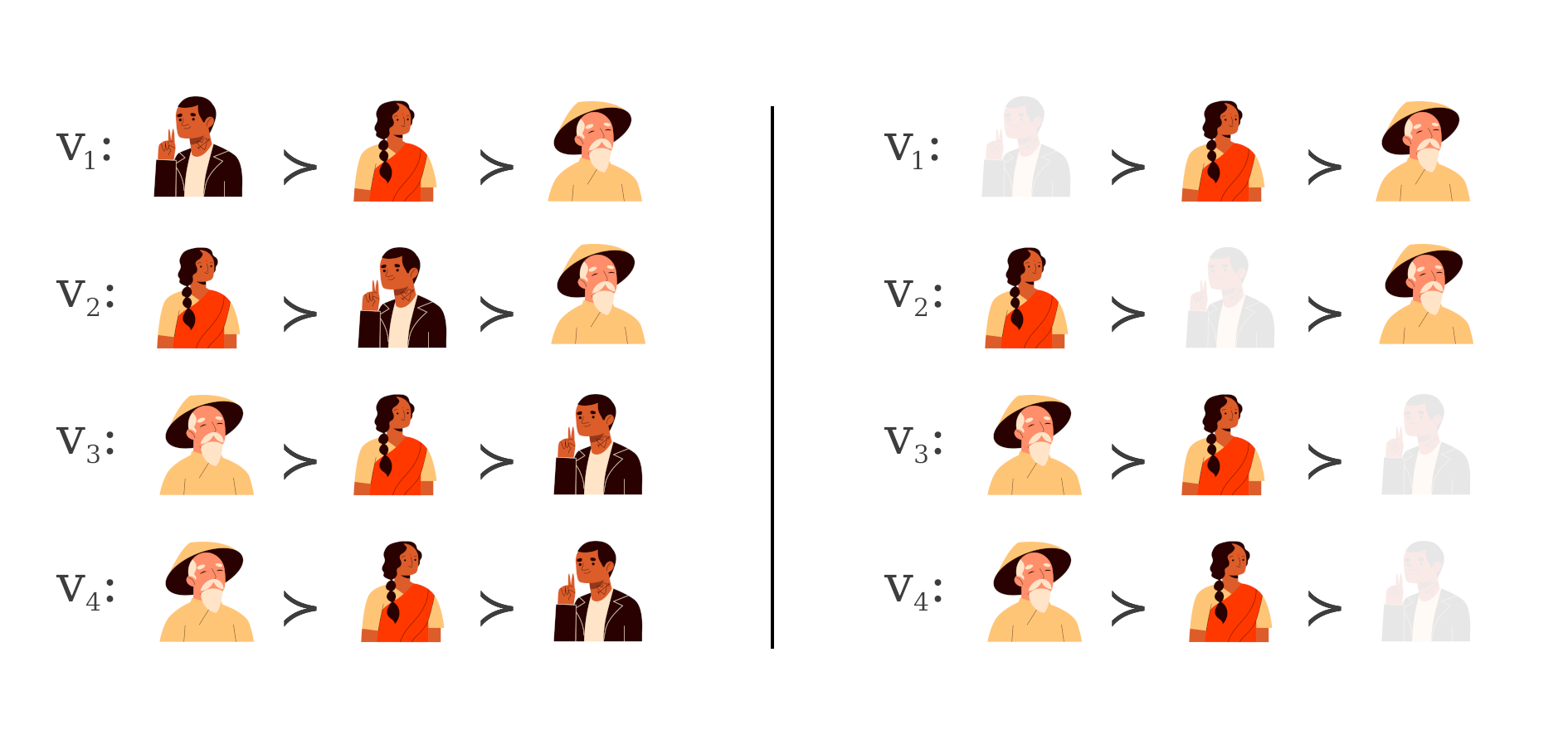
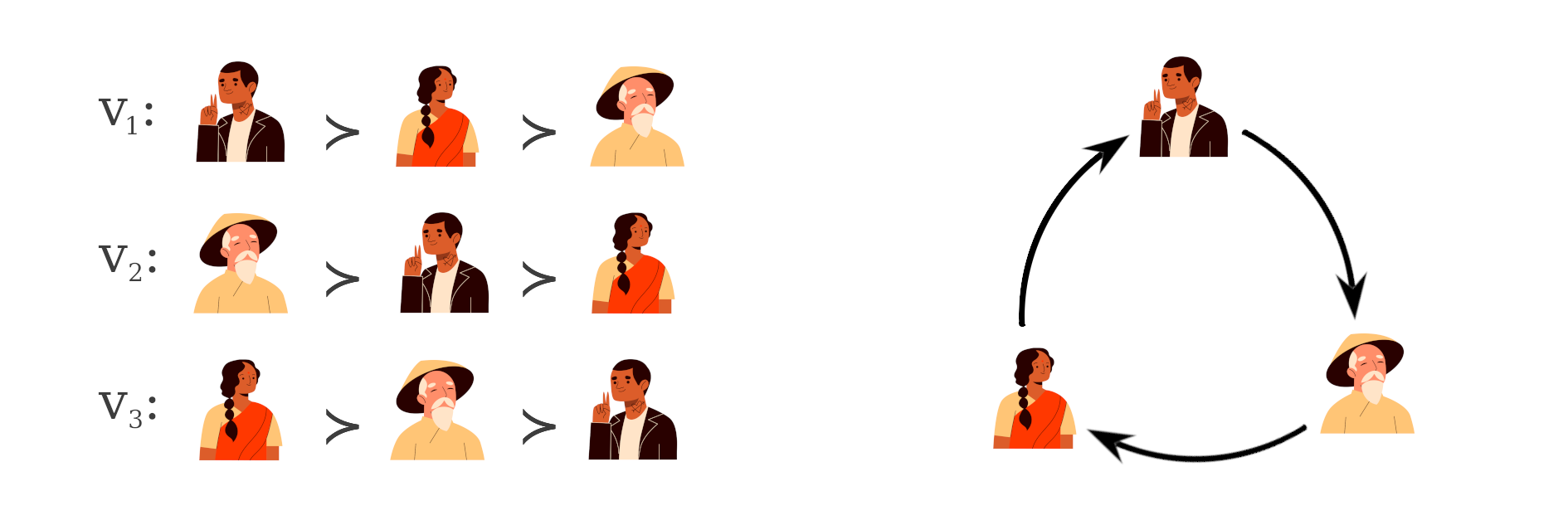
Let's look at another SWF that appears to address the issues with the plurality rule. The Copeland rule: candidate who wins the largest number of pairwise majority contests is declared as the winner. Under this rule, considering the example above, Rani wins against Liu and draws with Paul. Liu and Paul does not win against any one. Therefore, Rani is the election winner. But the Copeland rule suffers from a different kind of problem - a majority cycle. If there were just three voters, and had they voted as shown below, there is no clear winner!
The Borda rule, The Baldwin rule, The Dodgson rule... There are so many more voting rules that we could discuss here. Each one of them comes with a solid argument for why it is the best voting rule. However, each one of them also highlights what is wrong with the other rules. This makes us wonder: what is it about voting rules that makes it so hard to come up with one that everyone agrees is correct? Is there something inherently impossible about voting rules?
Arrow's take on voting rules
Arrow starts with formally stating some of the basic properties that any reasonable voting rule must satisfy. When you see them, I am sure that you too would say duh? obviously🤷.
- Firstly, If every single voter strictly preferes candidate \(a\) over candidate \(b\), i.e., \(\forall i\in{N}, a\succ_i{b}\), then the voting rule must rank \(a\) higher than \(b\),i.e., \(a\succ{b}\). Such an SWF is said to be weakly Paretian. This is also referred to as unanimity.
- Secondly, for any two candidates \(a,b\in A\), the relative ranking of \(a\) and \(b\) in the social preference order \(\succeq\) should only depend on the relative ranking of \(a\) and \(b\) by the voters, but not, for instance, on how the voters rank some third candidate \(c\). we call such voting rules independent of irrelevant alternatives (IIA). Note that our toy example shows why the plurality rule is not IIA. The ranking of Rani and in the social order depends on how the voters rank Paul.
- And lastly, a voting rule should not be a dictatorship. An SWF is said to be dictatorship if there exists a voter \(i^*\in N\) (the dictator) such that for any two candidate \(a,b\in A\), \(a\succ_{i^*}b\) implies \(a\succ{b}\). That is, the SWF simply copies the strict ordering on the dictator completely ignoring other's preferences. Note that a dictatorship is both weakly Patetian and IIA. What Arrow proves is that the converse is also true
Arrow's Theorem (1951): When there are three or more alternatives, then every SWF that is weakly Paretian and IIA must be a dictatorship.
Proof [Simplified version- Sen, 2014]: Let \(|A|\ge 3\) be a set of candidates and let \(f\) be any SFW that is weakly Paretian and IIA. Let's begin with defining a few notions. A subset of voters is called as a coalition. A coalition is said to be decisive over an ordered pair \((a,b)\) of alternatives for \(f\) if and only if when every voter \(i\) in the coalition ranks \(a\succ_i{b}\) then the outcome of \(f\) is \(a\succ{b}\). A coalition is decisive if it is decisive for all ordered pairs. Lastly, we call a coalition weakly decisive over an ordered pair \(a,b\), if and only if when every voter \(i\) in the coalition ranks \(a\succ_i{b}\) and every voter \(j\) outside the coalition ranks \(b\succ_j{a}\) then the outcome of \(f\) is \(a\succ{b}\).
To prove this theorem, we first show that for the arbitrarily chosen welfare function \(f\), there is a decisive coalition - meaning there is a subset of voters who fully decide the outcome of the election. This is called as the Field expansion lemma. Once this is established, we show that this decisive coalition can be repeatedly shrunk until we get a singleton set - a hidden dictator among the voters who decides the outcome.
Field Expansion Lemma: If a coalition \(G\) is weakly decisive over \((a,b)\) for some \(a\neq{b}\), then it is decisive.
Proof: Let \(G\) be weakly decisive over \((a,b)\) for some SWF \(f\). Let \(c\) be some candidate other than \(a\) or \(b\). Consider any profile where every voter \(i\) in the coalition \(G\) ranks \(a\succ_i{b}\succ_i{c}\), and every voter \(j\) outside the coalition \(G\) ranks \(b\succ_i{a}\) and \(c\). As \(G\) is weakly decisive over \((a,b)\), we have \(a\succ{b}\) in the outcome. Since \(f\) is weakly Paretian, we have \(b\succ{c}\) in the outcome as all the voters unanimously agree on this. Therefore, we have \(a\succ{c}\). Now, since \(f\) is IIA, the outcome \(a\succ{c}\) is dependent only on the relative ranking of \(a\) and \(c\) by the voters. That is, in all the profiles where \(G\) ranks \(a\suc_i{c}\) for each \(i\) in \(G\), the outcome is \(a\succ{c}\). Therefore, \(G\) is decisive (not just weakly) for \((a,c)\). Similarly, we can show that \(G\) is decisive over \((c,b)\). With the help of these two claims, we can show that \(G\) is decisive for any pair in \(\{a,b,c\}\). Repeating this process, we can iteratively expand this set to show that \(G\) is in-fact decisive over all pairs of candidates: \(G\) is decisive. \(\square\)
As \(f\) is weakly Paretian, It is clear that the entire set of voters \(N\) is decisive. We not have our initial decisive coalition - the entire set of voters. Let's now contract it using the Group contraction lemma as follows.
Group contraction Lemma: If a coalition is decisive, and has size \(\ge{2}\), then it has a proper subset that is also decisive
Proof: Let \(G\) be a decisive coalition of size \(\ge 2\). Partition \(G\) into two non empty subsets \(G_1,G_2\). Fix distinct candidates \(a,b\) and \(c\). Consider any profile where the relative ranking of these candidates are in a cyclic manner as given below:
voters in \(G_1\) : \(a\succ_i{b}\succ_i{c} \\\) voters in \(G_2\) : \(c\succ_i{a}\succ_i{b}\\\)voters outside \(G\) : \(b\succ_i{c}\succ_i{a}\)
Since \(G\) is decisive, the outcome has \(a\succ{b}\). We know that in the outcome either \(a\succ{c}\) or \(c\succ{a}\). If \(a\succ{b}\) Then \(G_1\) is weakly decisive over \((a,c)\) and applying the field expansion lemma, \(G_1\) is decisive. Otherwise, if \(c\succ{a}\), since \(a\succ{b}\), we have \(c\succ{b}\). This makes \(G_2\) weakly decisive over \((c,b)\) and therefore decisive. Therefore, we have shrunk the decisive coalition. \(\square\)
Having these two lemmas, starting with \(N\) and repeatedly applying the Group contraction lemma contracts the coalition to a singleton set - a dictator. \(\square\)
Since Arrow's result, the field of social choice theory has expanded significantly, resulting in a substantial body of research. I will be writing about intriguing results in social choice theory - especially the computational aspects of it.
TLDR? watch this 30 sec summary of what democracy is by Osho ;)